“誤解を招く表現”に騙されない方法 推論力で悪意から身を守る

　と友人が儲け話をうちかけられ、妙に説得力ある内容にアナタはすっかりその気になり儲け話に乗ってみたら散々な結果に。後日友人を問い詰めると――

　なんてすっとぼけた顔で言われた経験、ありませんか？

　世の中にはこういった“誤解を招く表現“を操る輩がたくさんいますね。ちょっとした損程度ならまだキズが浅くてすみますが、もしひと財産かけるような規模だったら取り返しがつかないことになります。相手にその気があったかどうかを確かめるのも難しく、結局アナタは泣き寝入りするハメに――こんな経験はしたくありませんよね？

　そういった“誤解を招く表現“を素早く察知するためには、冷静かつ的確な『思考力』が必要不可欠です。今回はそんな誤解を招く表現を操る輩に論破されないための『論破されない思考力』を鍛える問題を紹介していきます。

思考に潜む罠　人間は都合が良い情報に目を向ける

　『思考力』には複数の種類が存在します。

　“誤解を招く表現”を操る輩は『推論』に対して罠を張り巡らせます。すでに知られている事実関係をもとに「じゃあ〇〇って□□だよね？」といった予測をたてる思考力で、悪意ある人はこの力を利用し曖昧な表現やハッキリとした意思を見せないことで後々のアドバンテージを得ようとしているのです。

　あらゆるテクニックを駆使する前に、そういった輩には『問題をハッキリさせること』を徹底させましょう。たとえば「〇〇だと思います」という表現ではなくハッキリと「〇〇です」という言質をとることなどが挙げられますね。

　他にも、曖昧な表現でうまく逃げようとする場合もあるでしょう。アナタ自身も「あれ？　これってもしかして違う意味だった？」と勘違いしてしまうパターンもあるでしょう。そういった勘違いを防ぐためにはどうすれば良いのでしょうか？

勘違いを防ぐ練習 “２-４-６課題”

　相手の表現にムダな誤解を産まないためには『早合点しない』ことが肝心です。そういった思考力を高めるため、イギリス出身の心理学者『ピーター・カスカート・ウェイソン』氏が考えた『2-4-6課題』をいっしょに考えてみましょう。

　これは『ある法則で並んだ数列の“法則を当てましょう“』という問題です。手法は以下の通りです

　ではさっそくはじめてみましょう。たとえば以下のような数列を提示されたとします。わたし(犬物語)が提示したとイメージすれば、より誰かとコミュニケーションしている風になるかもしれません。

　この数列はどのような法則で並んでいるでしょうか？　よく考えてアナタも同じように数列を挙げてみてください。アナタが提示した数列が法則を満たしているならわたしは「Yes」と答え、満たさないのであれば「No」と答えます……まあこれはブログ記事ですし実際にコミュニケーションがとれるわけではないので、下に予測される数列を並べ、出題者の答えも一緒に載せておきます。

　どうでしょう？　法則は導き出せましたか？　画像の後に答えを提示するのでちょっとだけ考えてみてください。

　この問題の“法則“の答えは『上昇系列』です。つまり左の数よりも大きい数字であればなんでもおっけーという法則で成り立つ数列ですね。アナタはもしかしたら「以前の数より2を足している」という予測をしたかもしれません。もし『1-2-3』という数列がリストにあったらそう勘違いせずに済んだかもしれません。誤解させてしまったとしたら申し訳ないですね。

真偽を確かめる能力

　人はある情報に囚われるとそのほかの情報をすべて無視するか、自分の都合の良い方向に解釈してしまいます(確証バイアス)。これは『真“偽“を確かめる質問』を考える判断力を鈍らせ、アナタが考えた“正しいこと“ばかりに意識が向いてしまい正しさだけを確かめるための質問だけをしてしまうのです。

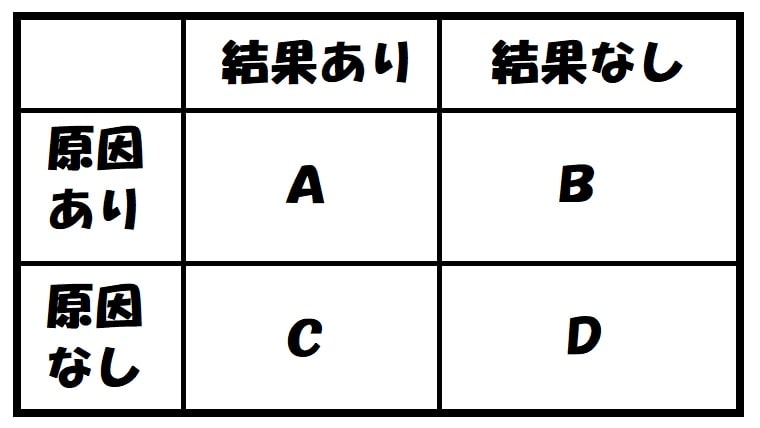
　誤解を招く表現をする輩はまさにその心理を突いてくるのです。ある評価を下したい場合、情報をできるだけ集め下記の『Ａ』に該当する情報源から慎重に検討していきましょう。また『D』に該当する結果も集めることで『法則に当てはまらない情報』を知ることできます。

※ある法則の”正しさ”を確かめたいならA・Dの是非を確認しよう

原因と結果の因果関係を見抜く練習 “４枚カード問題”

ここでちょっと有名な認知バイアスの問題である『4枚カード問題(ウェイソン選択課題)』に登場してもらいましょう。以下の画像を御覧ください。

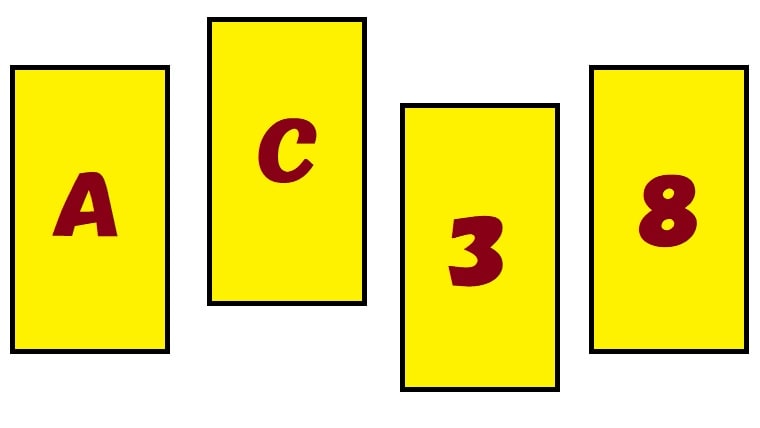
　このカードは『表が母音(A,E,I,O,U)ならば裏は偶数』というルールの上でそれぞれ数字とアルファベットが記されています。ですが疑り深いアナタはそれを確かめなければ気が済みませんよね？　そこで最低限の数カードを裏返してルールに沿っているかどうかを確認してみましょう！

　ここでポイントとなるのは以下の通りです。

　もう1度画像をお見せしますのでちょっぴり考えてみてください。

　わかりましたか？　もしかして『A・８』のカードを選んでしまったのではないでしょうか？　それは半分正解です！　――では早速答えと解説を書いていきましょう。

　答えは『A・3』のカード2枚です。

　ルールの『表が母音ならばその裏は偶数』に着目しましょう。これは以下のことが言えますね。

　母音のカードをめくれば設定されたルールが正しいか確認できます。問題はその後で、ルールから逸脱した禁じられたルールを確かめる必要がありますね。ちょっと難しい内容ですが論理学的な考え方を紹介しましょう。

　表が母数を『P(前件)』、裏が偶数を『Q(後件)』とすると、これは『P → Q』の式で表すことができます。この条件の確かさを検証するためには、PとQの関係性が正しいかを検証しなければなりません。すなわち以下の要素を確かめる必要があります。

　上を『前件肯定』、下を『後件否定』と呼びます。

　この作業を行えば最小限のカードをめくることができるのです。あるルールが正しい時『成立しないルール』についても考える。これが論理的思考の肝になります。知っておくと相手に論破されない理論構築が可能となりますのでぜひ備えておくようにしましょう。

　論理的思考は論破されないだけでなく問題解決能力の向上や認知バイアス対策にもなります。相手の“誤解を招く表現”に騙されず逆に論破する勢いで張り切っていきましょう！

Bitly

amzn.to